عندما تصبح المجاميع غريبة في اللانهاية

 عندما نقوم بعمليات الحساب في اللانهاية، تصبح الأمور غريبة بعض الشيء، فقد نحصل على أعداد مختلفة لمجموع نفس القيم، وقد تتغير هذه القيم فقط بتغيير ترتيب هذه العناصر (رغم أننا نعلم أن الجمع تبادلي، أي يجب الحصول على نفس النتائج عند تغيير ترتيب هذه الأعداد)

فلنتسلى قليلا في اللانهاية، ولنعتبر المجموع اللامنتهي :

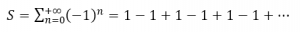
يسمى هذا المجموع  Grandi’s series  أو سلسلة غراندي، فإذا قمنا بعملية الجمع على هذه الشاكلة:

فمن السهل استنتاج أن S=0 لأنها عبارة عن مجموع أعداد منعدمة 0=(1-1)،

أما إذا قمنا بتجميع القيم على شكل آخر:

فإننا نحصل على مجموع يساوي 1، إذا يمكننا استنتاج أن هذا المجموع يمكن كتابته على الشكلين:

فكل ما فعلناه هو إضافة 0 للمجموع، أي أننا لم نغير شيئا من قيمتها.  فلنجمع الآن الحدود مع بعضها البعض  بهذه الطريقة:

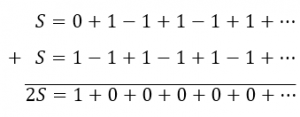
فنحصل على أي  ، وهذه قيمة ثالثة لنفس المجموع ! مما يدعو للإستغراب، فكل ما قمنا بفعله منطقي، لكنه لا يعطي نفس القيم لأنه مجموع لا منته، وهذا ما يدعو للغرابة.

مثال آخر لمجموع لامنته: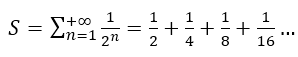   

هناك عدة طرق لحساب هذا المجموع، فعلى سبيل المثال، يمكننا الإستعانة بالتمثيل التالي:

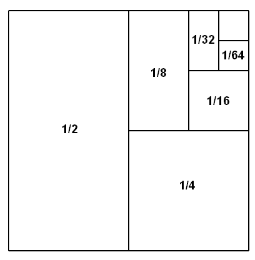
في مربع ضلعه يساوي 1 (وحدة  قياس)، لدينا: مساحة نصف المربع هي ½  و مساحة ربعه هي ¼ أي نصف النصف ½ ،  ثم ⅛ أي نصف ¼  ونكمل على نفس الوثيرة إلى مالا نهاية، فنحصل في الأخير على مجموع هذه المساحات هو 1

يتفق الرياضيون مع هذا التحليل لأن لهذا المجموع قيمة محددة، أو بعبارة رياضية: هذه السلسلة متقاربة، يمكننا أيضا القيام بجمع البعض من تلك القيم والحكم عليها، فلدينا هنا:

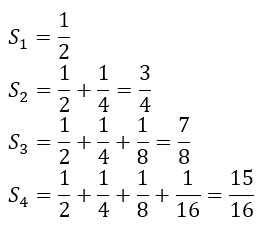
وهكذا، نحصل على قيم تقترب من 1، لذا نقول أن هذه السلسلة متقاربة لأنها تقترب من قيمة واحدة عكس سلسلة غراندي فهي متباعدة لأنها لا تقترب من قيمة محددة وثابتة.

المصدر: [1]