توجد الرياضيات في كل شيء، وتستطيع وصف أي شيء في حياتنا دون أن نشعر بها، وفي الطبيعة دون أن نستوعب ذلك، ضمن سلسلتكم الرياضيات والعالم، سنربط في مقالتنا هذه الطبيعة ومجالات أخرى بالفراكتال أو الهندسة الكسيرية وكذا بالأعداد العقدية والمتتاليات العددية. سنة 1975، أضاف العالم كلمة جديدة لقاموس الرياضيات، ألا وهي الفراكتال، فما هو الفراكتال وما هي أهميته؟
“الفراكتال” هي أشكال هندسية متماثلة، بحيث نجد نفس التفاصيل عندما تُغير مسافة رؤيتها كما هو موضح في الصورة، وكان أول من وضع كلمة “فراكتال” العالم الرياضي “بينوا مانديلبروت“، وقد بدأ العالم باستخدام تلك الأشكال المميزة والملونة عن طريق الحاسوب خلال الثمانينات، لكن سرعان ما غيرت هذه الهندسة الكسيرية، منظورنا للأشياء، فهي تحمل جمالا عميقا وقوة كبيرة للأفكار.
 wikimedia Sierpinski Fractal
wikimedia Sierpinski Fractal
وأفضل طريقة لإدراك جمالية الفراكتال، هي النظر في بعض الأمثلة، كالغيوم والجبال والسواحل والقرنبيط وغيرها، فكلها فراكتالات طبيعية، وهي تشترك في أمر بديهي: الجمال، فإذا ما نظرنا عن كثب في الطبيعة فسنجد تعقيدات كثيرة في التفاصيل، فمثلا تتكون شجرة الصنوبر من فروع والتي بدورها تتألف من فروع أخرى، وهذا هو الفراكتال، فمن العبارات الشهيرة للعالم مانديلبروت الذي حاول وصف الطبيعة باستعمال الفراكتال: “الغيوم ليست فِلكات، والجبال ليست مخاريط، والخطوط الساحلية ليست دائرية، ولحاء الشجر ليس أملس، ولا يشق البرق طريقه وفق خط مستقيم”، لذا يعتبر الفراكتال من الأشكال المعقدة وغير المنتظمة وبالتالي يصعب وضعه ضمن معادلات كباقي الأشكال المنتظمة مثل الدائرة.

يمكن أيضا القول أن الفراكتال ونظرية الفوضى تلهمان العديد من العلماء في الكثير من التخصصات، كعلم الكون والطب والهندسة وعلم الوراثة وغيرها من المجالات، فالعالم كله عبارة عن فراكتال، وهو يُمكِّننا من فهم بعض الأنظمة المعقدة كتوقيت وحجم الزلازل والتغير الذي تعرفه ضربات قلب شخص معين وحتى في تشخيص بعض الأمراض ، بالإضافة إلى تطبيقاته المتنوعة في إنتاج رسومات مذهلة وواقعية عبر الحاسوب، وفي ضغط ملفات الأنظمة وهندسة شبكات الأنترنيت وحتى في الأسواق المالية، حيث اكتشف مانديلبروت لأول مرة التعقيد الرياضي للفراكتال خلال عمله بشركة IBM في الستينات، فحاول وصف السوق التجاري باستخدام رياضيات الفراكتال.
يوجد العديد من أنواع الفراكتال، لكن هناك مجموعة كبيرة تخضع للمتتالية العقدية الترجعية (Zn) والتي اشتغل عليها مانديلبروت:
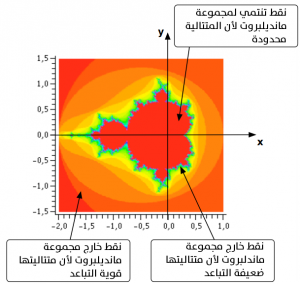
ونسمى مجموعة مانديلبروت كل الأعداد العقدية c التي من أجلها المتتالية (Zn) تكون محدودة (أي محصورة)، هذه المتتالية تمكن من خلق أشكال مذهلة باستعمال برانم خاصة (كالصورة أسفله، والتي صممت باستعمال البرنام Maple).
المصادر: BBC و École Polytechnique de Montréal و library.uvawise
الكاتب:
المدقق اللغوي: