تُعتبر الرياضيات لغة العلوم، وقد وصفها الفيزيائي والفلكي “غاليليو غاليلي” في مقولته الشهيرة: “الرياضيات هي اللغة التي كتب بها الإله الكون”، كما يقول في كتابه ( Opere Il Saggiatore) : “[الكون] لا يمكننا قراءته دون تعلم وفهم اللغة التي كُتِب بها. إنه مكتوب بلغة الرياضيات، فالحروف هي المثلثات والدوائر والأشكال الهندسية الأخرى، وبدونها لا يمكن للإنسان فهم كلمة واحدة”
فهل يمكننا اعتبار الرياضيات كلغة مثل الإنجليزية أو الصينية؟
للإجابة عن هذا السؤال يجب استيعاب ما هو تعريف “اللغة”؟ وكيف نستعمل المفردات والقواعد في الرياضيات لتكوين جمل ذات معنى؟
ما هو تعريف اللغة:
هناك عدة تعاريف للغة، فقد تكون مجموعة من الكلمات والشيفرات المستعملة بطريقة معينة، وقد تُعَرَّف أيضا على أنها نظام تواصلي يَستعمِل الحروف الصوتية، لكن عالم اللسانيات “نعوم تشومسكي” يعطي تعريفا أدق، فاللغة هي كتلة من الجمل المكوَّنة من مجموعة من العناصر المحدَّدَة. كما يعرفها علماء لسانيات آخرون على أنها يجب أن تتمكن (اللغة) من وصف الأحداث والمفاهيم المجردة.
مهما كان التعريف المستعمَل، فللغة مكونات محددة:
- يجب أن تتوفر على مفردات (سواء كانت عبارة عن كلمات أو رموز) (Vocabulary)
- يجب أن تَحمِل هذه المفردات معنى (Meaning)
- يجب أن تتحكم فيها قواعد تضبط كيفية استعمالها (Grammar)
- يجب أن تخضع المفردات لتسلسل منظم لتكوين جمل مفيدة (Syntax)
- يجب أن يتكون الخطاب من مجموعة من الجمل المتسلسلة (Discourse or Narrative)
- وأخيرا، يجب ان يكون هناك أشخاص يستعملونها ويفهمون مفرداتها.
تحقق الرياضيات كل هذه الشروط، وهي تتكون من مفردات ومعانٍ وقواعد يفهمها العالم بأسره، و يستعملها الرياضياتيون والعلماء وآخرون لتوصيل المفاهيم، فالرياضيات تشرح نفسها (الميتارياضيات Metamathematic : فرع يدرس الرياضيات) وتشرح ظواهر العالم والمفاهيم المُبْهَمَة.
مفاهيم وقواعد الرياضيات:
تأتي مفاهيم الرياضيات من العديد من الحروف والرموز الخاصة بها، فمثلا، يمكن لمعادلة رياضية أن تُكتب على شكل كلمات لتعطي جملة مكونة من أسماء وأفعال، كالمعادلة: 3+5=8 والتي تعطي “ثلاثة زائد خمسة تساوي ثمانية” أو “إذا أضفنا ثلاثة إلى خمسة فإننا سنحصل على ثمانية”، وبالتالي، فالرياضيات تضم كلا من:
- الأعداد (1 ; 102)
- الكسور (1/2 ; 5/71)
- المتغيرات (x ;y ;z ; a ; b ;c)
- التعابير (x² ; x+3 )
- المخططات (دوائر، المصفوفات، زوايا، رسوم مبيانية)
- اللانهاية
- العدد “باي” ( π)
- الأعداد التخيلية (i, -i)
- سرعة الضوء (c)
- …
وتضم أفعالها:
- المعادلات والمتراجحات (= ; < ; >)
- العمليات (الجمع، الضرب…)
- وأشياء أخرى (sin, tan, sec)
لذا يمكننا الحصول على جمل مفيدة في الرياضيات تضم الأفعال والنعوت والعطف…كل حسب مضمون النص، وهو محتوى عالمي، فمهما كانت اللغة التي يتحدث بها القارئ يمكنه فهم لغة الرياضيات ونصوصها، لأنها تستعمل نفس القواعد:
- تُقرأ النصوص من السيار إلى اليمين
- تستعمل الحروف بطرق مختلفة حسب دلالة كل منها في النص (بصفة عامة: تعبر الحروف اللاتينية والإغريقية على “البارامترات” والمتغيرات، والحروف i, j, l, m, n على الأعداد الحقيقية، a, b, c على الأعداد الحقيقية، z ;w على الأعداد العقدية، x ; y ; z على المجاهيل، و f ;g ;h على الدوال)
- تستعمل الأقواس والمعقوفات للحفاظ على ترتيب العمليات
- تنهج نفس الطرق للتعامل مع الدوال، والتكامل، والاشتقاق.
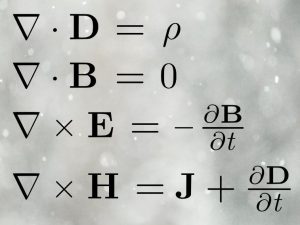
معادلات ماكسويل
رغم كل ما تحققه الرياضيات من شروط اللغة، إلا أن البعض لا يتفق مع تسميتها كذلك، وذلك بحجة أنه من بين تعاريف اللغة أنها تستعمل للتواصل الشفوي، بينما تستعمل الرياضيات فقط على شكل كتابي، صحيح أنه يمكن قراءة بعض النصوص شفهيا وبطريقة بسيطة ( كالعملية: 1+1=2 ) لكن بعض النصوص صعب للغاية (كمعادلات “ماكسويل”)، كما أن هذه العبارات تُقرأ حسب لغة القارئ وليست لديها طريقة قراءة موحدة عالمية.
ولأن الرياضيات هي نفسها في العالم بأسره، فإنها لغة كونية، لأن عبارة رياضية تحمل نفس المعنى في كل بقعة من بقاع العالم ومهما كانت اللغة التي تصاحبها. بفضل هذا، تساعد الرياضيات على التعلم والتواصل رغم كل الحواجز والفوارق التي يمكن أن توجد.
المصدر [1]
الكاتب:



