هل تساءلتم يوما إذا ما كانت الرياضيات أكثر تعقيدا في الماضي؟ كثيرون يشتكون من صعوبة فهم الرياضيات، لكن أؤكد لكم أنكم بعد قراءة هذا الموضوع ستتراجعون عن أحكامكم، فقد كانت الرياضيات أكثر تعقيدا، والآن هي مبسطة بشكل يمكن لأي شخص فهمها.
كانت الأعداد الكسرية تكتب بطريقة مختلفة عن التي عهدناها، فعندما يتواصل ذكر الأعداد فهذا يعني القيام بعملية الضرب، أما إذا وضعت “و” بين الأعداد فهذا يعني عملية الجمع، و”إلا” تعني عملية الطرح، مثال: “سبعة أثمان أربعة أخماس الثلثين” وهي تكتب على الشكل 
وهذا يعني 
أما العبارة “ثلاثة أرباع وخُمُسان وستة أسباع الخمس” فتكتب على الشكل 
وهي تعني 
سنرفع التحدي قليلا، هل تستطيعون قراءة العبارة التالية رياضيا: “ثلاثة أثمان وخمسة أسداس الثمن و أربعة أسباع سدس الثمن“، هذه العبارة تكتب 
وهي تعني: 
سأترك لكم الكتابة التالية لتحللوها: “خمسة أسباع وثلث السبع إلا ثمنها وأربعة أخماس الثمن” قد تجدون الأمر ممتعا، لكننا حاولنا تبسيط النصوص قدر الإمكان مع اختيار العبارات الأسهل للفهم، فهناك نصوص معقدة جدا في كتب الخوارزمي،
سننتقل الآن إلى المعادلات، فقد أطلق الخوارزمي أسماء عدة للدلالة على وضع مجهول في معادلة، فقد كان يسمي المجهول
الذي نَعرِفُه باسم “شيء” أو “جذر“، و 
باسم “مال” أما 
فاسمها “كعب”، لذا فعندما يكتب الخوارزمي: “أموال وجذور تعدل عددا، وأموال وعدد تعدل جذورا، وجذور وعدد تعدل أموالا” فهو يقصد المعادلات التالية على التوالي:
و 
و 
.
هل تستطيعون تحليل هذا النص: “25 كعب كعب و9 أموال مال و84 مالا و64أحادا و 100 جزء مال و64 جزء مال مال إلا 30 مال كعب و40 كعبا و116 شيئا و48 جزء شيء و96 جزء كعب”
هذا النص عبارة عن نص رياضي يضم المجهول وهو يعني: 
كما أن الخوارزمي تمكن من صياغة حل للمعادلة: 
وذلك بطريقة هندسية، فقد اعتمد على مربع مساحته ، ثم أضاف إليه أربعة مستطيلات مساحة كل واحد منها 
، ثم نكمل الأطراف بمربعات صغيرة مساحتها 
للحصول على مربع كبير كما هو ممثل في الشكل:
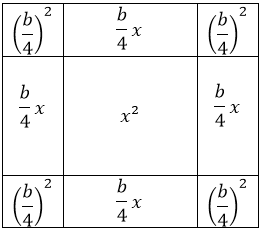ومنه فإن مساحة المربع الكبير هي:
وبما أن: 
فإننا نحصل على: 
بالتالي يكون حل المعادلة هو:
وهكذا يكون الخوارزمي قد حل المعادلة من الدرجة الثانية على الشكل .
تصوروا معي لو كنا نستعمل هذه العبارات والكتابات في دراسة الرياضيات! أليست الرياضيات أسهل بكثير حاليا؟ تجدر الإشارة إلى أن هذا المقال يبرز فقط صعوبة قراءة النصوص الرياضية، أما حل المعادلات، فقد كان أعقد بكثير من ذلك، لذا نعود ونقول إن الرياضيات اليوم قد قطعت أشواطا كبيرة جدا لتصل إلى البساطة التي نعرفها الآن من إمكانية حلول المعادلات، والمتراجحات، والنظمات إلى الهندسة، والجبر، والتحليل.
المراجع:
- كتب الخوارزمي: تأسيس علم الجبر(سلسلة تاريخ العلوم عند العرب – مركز دراسات الوحدة العربية –بيروت 2010) و كتاب الجبر والمقابلة (سلسلة العلوم في تراث الإسلام – لبنان – 2008)
- درس مقدمة حول ابستمولوجيا الرياضيات، للأستاذ الجامعي الزعيم لعبيد، أستاذ بجامعة القاضي عياض.
- الصورة [1]
الكاتب:
المدقق اللغوي:
