الأعداد الحقيقية:
نتعامل مع الأعداد الحقيقة كل يوم وكل دقيقة، لكن وربما لم يسبق لنا أن طرحنا على أنفسنا السؤال التالي:
ما هي الأعداد الحقيقية بالضبط؟
ربما تكون الإجابة الأكثر بديهية أن الأعداد الحقيقية هي الأعداد التي توجد على المستقيم العددي، بما في ذلك الأعداد الصحيحة، والتي تبعد عن بعضها البعض بنفس المسافة، هناك أيضا أعداد أخرى مثل: 1.4 و0.33 والتي هي الأخرى تبعد عن بعضها البعض بمسافة معينة:
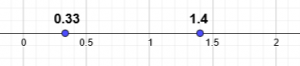
هذه الأعداد، والتي يمكنها أن تتكون من عدد منتهي من الأرقام بعد الفاصلة مثل: 7/5 = 1.4 أو من مجموعة لامنتهية من أرقام متكررة مثل: 1/3 = 0.333… تسمى أعدادا جذرية، كلها تكتب على شكل أعداد كسرية. في المقابل، هناك أعداد لاجذرية مثل: …3.141592=Π و …1.41421=2√ والتي تتكون من أرقام لامنتهية وغير متكررة بعد الفاصلة ولا تكتب على شكل كسر !
نحن في الحقيقة لا نملك تعريفا خاصا لمثل هذه الأعداد الحقيقية! وهذا ما يجعل الأعداد اللاجذرية أكثر تعقيدا مما نتصوره، لأن عقولنا وأدواتنا المحدودة لا تُمَكِّنٌنا من تحديد هذه الأعداد على المستقيم العددي، لذا نلجأ للعمل بالتقريبات، فمثلا، عندما نستعمل العدد Π فإننا نربط قيمته بمدى دقة المستوى الذي نشتغل فيه، فقد نستعين بالتقريب 3 أو التقريب 3.1 أو3.14 أو 3.141 ألخ… فكلما أضفنا رقما كلما حصلنا على دقة أفضل.

الأعداد الموجودة بهذه السلسلة تتكون من أرقام محدودة وراء الفاصلة أي أنها أعداد جذرية، لذا، عمليا، نُكَوِّن متسلسلة أو بالأحرى متتالية من أعداد جذرية تعطي في كل حد لها تدقيقا أكثر فأكثر للعدد Π والتي تكون نهايتها هي Π بالضبط. بنفس الطريقة يمكن تحديد أعداد حقيقية-لاجذرية أخرى.
هناك طريقة أخرى لاستيعاب مفهوم الأعداد الحقيقية، فبدلا من تحديد أرقامها اللامنتهية وراء الفاصلة يمكن تمثيلها بمتتالية لأعداد جذرية والتي تؤول إليها، فمثلا مع Π، يمكننا تحديده باستعمال متتالية الأعداد الجذرية التالية:
![]()
أو ![]()
يبقى هذا التعريف صالحا أيضا لتعريف باقي الأعداد، فمثلا، إذا اعتبرنا المتتالية: 1 ;1 ;1 ;1 ;… فإنها تؤول إلى 1 بكل وضوح، لذا يمكن تمثيل العدد 1 بهذه المتتالية.
متتالية “كوشي”:
ليست جميع المتتاليات المكونة من أعدادا جذرية تؤول إلى عدد حقيقي، فمثلا المتتالية: 1 ;2 ;3 ;4 ;5… تؤول إلى مالا نهاية، لذا سنُعَرِّف متتالية خاصة ستساعدنا في رؤيتنا الجديدة للعدد الحقيقي. لنعتبر متتالية بحدود عشوائية بحيث تكون هذه الحدود متقاربة فيما بينها، وللمزيد من الدقة، لنأخذ عددا موجبا صغيرا جدا نسميه ε بحيث كلما زدنا حدودا جديدة في المتتالية كلما كان الفرق بينها يصغر ويصغر ويقترب من ε، هذه المتتالية تسمى “متتالية كوشي” « Cauchy sequence » وهي تتميز بكونها تؤول إلى عدد حقيقي، وهكذا يمكننا القول بأن كل متتالية من متتاليات “كوشي” تُعَرِّفُ عددا حقيقيا، وعكسيا، كل عدد حقيقي هو نهاية لمتتالية من متتاليات “كوشي” المكونة من أعداد جذرية، وهكذا نكون قد أعطينا معنىً للأعداد الحقيقية على شاكلة متتالية “كوشي”.
لماذا نفعل كل ذلك؟
سؤال وجيه ! أول ميزة تتمتع بها متتالية “كوشي” هي كونها سهلة الفهم ومبسطة على شكل أعداد جذرية، فمن السهل تخيل أعداد جذرية تقترب من بعضها البعض كما شهدنا في المثال السابق مع متتالية العدد Π ، أما من ناحية أخرى، فهي تتميز بخصائص الجمع والضرب التي تتمتع بها الأعداد الحقيقية. تخيلوا معي مثلا أننا نريد جمع العددين …3.141592=Π و …1.41421=2√ ، لا يمكننا القيام بعملية الجمع بهذه البساطة، فالرقم الرابع وراء الفاصلة للعدد 2√+ Π لا يساوي جمع الرقمين الرابعين من العددين Π و 2√ لأن 7=2+5 لكن المجموع الفعلي يعطي 8 (لأننا أضفنا 1 من مجموع الرقمين السابقين على اليمين، وبصفة عامة، يمكن إضافة أعداد أكبر من 1 في كل مرة). لكن متتالية “كوشي” لا تخلق مثل هذه المشاكل، فحينما تجمع أو تضرب حدين من نفس الرتبة فهو يعطي تماما الرقم المطلوب في العملية، وبهذا تُسهِّل هذه المتتالية العمليات الحسابية بشكل كبير، وخصوصا النظرية منها.



