الرياضيات وفن الغرافيك
لطالما ارتبطت العلوم بالرياضيات، فالرياضيات تعد عمودا وأساسا مهما للعلوم الأخرى بحيث تضمن لها الدقة اللامتناهية، لكن تطبيقات الرياضيات تتعدى العلوم إلى مجالات أخرى، سنختار لكم اليوم التحدث عن علاقة فن الغرافيك بالرياضيات.
[image1]
لا شك أنكم سألتهم عن مدى أهمية دراسة فرع الهندسة متعددة الأبعاد 
وعن وظيفة المتجهات 
والمصفوفات 
والمُميّزات 
وغيرها من المصطلحات الرياضية، ببساطة، لو لم توجد هذه المفردات الدقيقة لما استطعنا استعمال فن الغرافيك لخلق صور وتصاميم وأشكال مميزة، سواءا أكانت ثنائية أم ثلاثية الأبعاد.
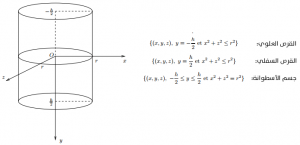
فمثلا، يمكن اعتبار أسطوانة عبارة عن اتحاد لقرصين علوي وسفلي وجسم الأسطوانة بالوسط، كل يتم التعبير عنه بمعادلة رياضية:
[image2]
تمكننا الرياضيات من كتابة اللوغاريتمات الصحيحة والمفصلة عن الأشكال التي نود ابتكارها باستعمال بعض البرانم، لكن من الضروري دراسة الهندسة المستوية والفضائية لتحقيق ذلك، فعبر معادلات بعض الأشكال كمعادلة الفلكة 
والدوال كالدوال المثلثية 
و 
تمكن من التحكم بالتصاميم وكذا إحداث التغييرات والتأثيرات المراد ابتكارها، أما المصفوفات فتمكن من تغيير المعلم المستعمل، فعندما نتحدث عن المعلم المتعامد الممنظم (أي منظم متجهات الأساس لها نفس القياس 
) والمباشر 
ليس كالحديث عن معلم متعامد غير ممنظم وغير مباشر بأصل مختلف عن أصل المعلم 
، هكذا نتمكن من تغيير إحداثيات متجهة أو نقطة من معلم لآخر دون تغيير موقعها في الفضاء!
[image3]
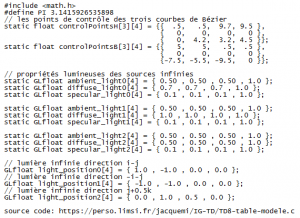
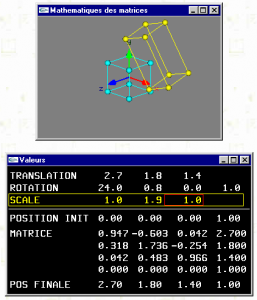
كالطاولة ثلاثية الأبعاد الممثلة في الفيديو، فقد تم استعمال برمجة مدروسة على برنام خاص، وهذا جزء صغير من البرمجة ( وهو يوضح استعمال المصفوفات والمتجهات لتحديد الشكل):
[movie]
أما أهمية الدوال فتتمثل في أنها تساهم في خلق نماذج هندسية معقدة، بحيث يتم دمج دوال عديدة من خلال استغلال تمثيلها المبياني للحصول على أشكال معقدة، سنعطي مثال الشكل أسفله الذي تم تحديده باستعمال كل من الدوال المثلثية قرص بواكريه “Poincaré disk” في الإحداثيات القطبية 
بالإضافة إلى بعض الدوال المعرفة بمجهولين كالدالة 
وبعض الدوال الشلجمية، إضافة لاستعمال الدوال الأصلية، كل ذلك تتم برمجته على الحاسوب ومن ثم طباعته بالطابعة ثلاثية الأبعاد التي غزت العديد من المجالات الأخرى كالطب والهندسة المعمارية والتكنولوجيا وغيرها.
