الرياضيات والتنبؤ بأحوال الطقس

تخيلوا معي إن لم يكن باستطاعتنا التنبؤ بأحوال الطقس ! ستكون كارثة، فلن نستطيع التحكم بظروف رحلاتنا الجوية والبحرية، أو التنبؤ بالكوارث الطبيعية من أعاصر وفيضانات للتمكن من اتخاذ الإحتياطات اللازمة، ولن نستطيع حتى تنظيم رحلاتنا العائلية، لذا يعتبر التنبؤ بأحوال الطقس والبحث في تطوير تقنيات تحديده بشكل أفضل من المسائل المهمة، ولا يمكن ذلك إلا بمساعدة الرياضيات.في إطار سلسلتكم ‘الرياضيات والعالم”. سنربط في مقالنا هذا الرياضيات بكيفية التنبؤ بأحوال الطقس، وسنرى كيف تقوم الرياضيات بضبط هذه التنبؤات.

تصرح الدكتورة “Hannah Christensen” من جامعة أكسفورد بأننا نسير نحو الأفضل للتنبؤ بأحوال الطقس نظرا للتقدم الذي عرفته الرياضيات والسرعة التي تعمل بها الحواسيب. سنشرح في هذا المقال  كيف بدأ العاملون بالأرصاد الجوية العمل بتقنيات رياضية وحواسيب متطورة لضمان الدقة في تحديد توقعات الطقس.

منذ عقود، وبالتحديد منذ سنة 1960، كانت التنبؤات بالأرصاد الجوية تعتمد أساسا على الملاحظة والسجلات المحفوظة، وقد كانت مهمة العامل بالأرصاد سهلة وبسيطة بحكم أنه يحدد طقس اليوم نفسه بمجرد الملاحظة، ليس كما هو الحال عليه حاليا بحيث يمكن التنبؤ بالأرصاد الجوية لأسبوع كامل، وبالتالي لم تكن هذه الطريقة ناجعة، لأنها لا تأخذ بعين الاعتبار نظرية الفوضى، فتطور الطقس من يوم إلى أسابيع حساس جدا للتفاصيل الدقيقة في الغلاف الجوي إلى درجة أنه لا يمكن كشفها باستعمال بيانات الأقمار الصناعية وبالونات الطقس المتاحة، لكن هذه الطريقة بقيت لمدة طويلة أفضل خيار متاح نظرا أن استخدام المعادلات لخلق نماذج رياضية لم تكن عملية حتى ظهور الكمبيوتر الإلكتروني.

أظهرت البحوث المقامة بقسم “دراسة الغلاف الجوي والمحيطات وفيزياء الكواكب” بجامعة اكسفورد أن الحصول على تنبؤات أفضل للطقس لا يختصر فقط على استخدام حواسيب أكبر لكن باستعمالها بطرق أذكى، ويصرح عالم الرياضيات “Lewis Fry Richardson” الإختصاصي في استخدام النماذج الرياضية أنه واجه صعوبة كبيرة  في تحديد توقعات الطقس للست ساعات المقبلة، فقد وجب عليه حل معادلات تفاضلية يدويا علما أنها تستغرق 6 أسابيع لحسابها بالحاسوب.

بدأت التوقعات الحديثة للطقس بالإعتماد على الرياضيات، وبالضبط بالمعادلات التفاضلية التي تصف تطور الغلاف الجوي:
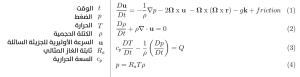تتكون هذه المعادلات من معادلة “Navier-Stokes” التي تصف حركة السوائل النيوتونية، وبذلك تمكن من وصف حركة تيارات المحيطات وحركة كتلة هواء الجو، وهي معادلة لم يتم البرهنة عليها رياضيا حتى الآن، لذا تعتبر هذه المعادلات جد صعبة لاحتوائها الإشتقاق D/Dt الذي يخفي بعض المصطلحات غير الخطية في u (يتوجب إذا فهم حلول معادلات “Navier-Stokes” التي لم تحل بعد والتي يخصص لها معهد كلاي للرياضيات ملايين الدولارات لحلها)، أما المعادلة الثانية فهي معادلة الإتصال “Continuity equation” والتي تصف الكثافة.و المعادلة الثالصة تصف الطاقة الحرارية حيث أن Q هو معدل التسخين، بينما ترتبط المعادلة الرابعة بحالة الطقس.

إذا للتنبؤ بحالة الطقس، يتم تقسيم الغلاف الجوي إلى مكعبات صغيرة بحجم 10×10 كم أفقيا وبضع المئات من الأمتار إلى بعض الكيلومترات عموديا، تتجلى ضرورة هذا التقسيم في استحالة معرفة حركة كل موجة صغيرة من الرياح، بعد ذلك يتم اتخاذ واحدة من هذه المكعبات كثابتة مع تحديد أعداد محددة تمثل درجة الحرارة والرطوبة وسرعة الرياح.

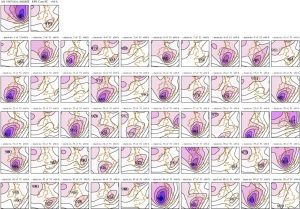
رغم كل هذا، فيجب أيضا دراسة عوامل أخرى كالغيوم التي تؤثر على بعض الظواهر الجوية مثل العواصف والمطر، لذا يتم استخدام المعادلات التقريبية المسماة بمخططات المعايير والثوابت “Parametrisation schemes”، غير أن هذه التقريبات قد تتكون من الكثير من الأخطاء، ولمعالجة هذا المشكل، بتم العمل على مخططات تحتمل العشوائية “Stochastic Parametrisation schemes” بتعبير آخر، تستعمل أيضا الإحتمالات.

من المستحيل التنبؤ 100% بأحوال الطقس، لكننا توصلنا اليوم لتوقعات جوية يمكن الإعتماد عليها بفضل الرياضيات والكمبيوتر، وتجدر الإشارة إلى أنه كلما حصلنا على حواسيب أكبر وأفضل كلما تحسنت توقعات أحوال الطقس.

المرجع: [1]