الرياضيات في مواجهة الوباء

يثير فيروس كورونا المستجد الخوف، فكما تظهر دراسة رياضية: ينتشر الوباء بشكل أسرع مما نعتقد، وهذا أمر مروع، لذا يضع وباء كوفيد 19 علم الفيروسات وكذا الرياضيات في الواجهة . 

إن النمو الأُسّي في عدد حالات الإصابة هو ما يجعل الموقف مُقلقًا للغاية: يتضاعف عدد المصابين دائمًا بعد نفس الفترة، قد لا يبدو هذا كثيرًا للوهلة الأولى ، لكنه يتحول في الحقيقة إلى أرقام مخيفة بسرعة كبيرة: من 17 مصابا يوم 14 مارس إلى ما يقارب 654 بحلول 1 أبريل، وبالتالي وجب اتخاذ التدابير الوقائية، بدءا بغسل اليدين والبعد الاجتماعي، وصولا للحجر الطبي للحد من انتشار المرض. 

الهدف هو إبطاء النمو الأُسّي وتحويل منحنى العدوى الذي يتزايد بشكل مُطَّرِد وأسرع فأسرع لجعله تناقصيا.

 يمكن وصف تطور الوباء ، بتقريب أولي، بالمعادلة التالية:

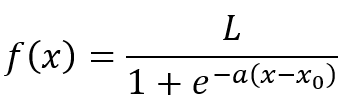
أو ما يسمى “المعادلة اللوجيستية”. تم تطويرها في عام 1838 من قبل عالم الرياضيات البلجيكي “بيير فرانسوا فيرهولست” (Verhulst) ، الذي عمل على النماذج الرياضية للنمو الديموغرافي، وذلك  نتيجة للعمل على “القانون الديموغرافي” الذي وضعه الاقتصادي البريطاني “توماس مالثوس” (Malthus)، والذي بموجبه يزداد عدد الأشخاص الذين يعيشون على الأرض بشكل كبير ، والذي يجب أن يؤدي عاجلاً أم آجلاً إلى كارثة، وبالتالي قام (Verhulst) بتحسين نموذج (Malthus) عن طريق إضافة مصطلحات رياضية إليه تمثل عوامل مختلفة يمكن أن تُؤطر نمو المنحنى. 

في حالة فيروس مثل (Covid-19) ، يكون النمو أُسّيًا في البداية. لكن من الواضح أن هذا لا يمكن أن يستمر إلى الأبد. في مرحلة ما ، سيستنفذ الفيروس موارده ، أي الأشخاص غير المصابين، لأن جزءًا كبيرًا من الساكنة مصاب بالفعل أو أصيب من قبل. ثم سيزداد عدد الحالات بشكل خطي، أي بشكل ثابت كل يوم،  وبالتالي سيتوقف نمو المنحنى تمامًا لاحقا، وهذا بالضبط ما تصفه المعادلة اللوجستية في الصيغة أعلاه ، فإذا كان x يشير إلى الوقت، فإن النمو الأسي يتوقف عند الوقت x0. أما الثابثة L فهي تشير إلى القيمة القصوى التي يمكن  للمنحنى الوصول إليها. ثم يأتي الرقم e وهو رقم “أويلر” (أو قاعدة اللوغاريتمات الطبيعية)، وأخيرا العدد k وهو العامل المضاعف الذي يشير إلى ميل المنحنى. 

لكن لدينا مشكلة، فانتظار انتشار الفيروس إلى حد عدم التمكن من العثور على الأشخاص المصابين الجدد سيكون بالنسبة لنا السيناريو الأكثر كارثية للوباء. هذا هو السبب الذي جعل العديد من البلدان تتخذ تدابير الحجر الصحي والتباعد الاجتماعي للحد من الاتصال بين الناس، والهدف هو الوصول إلى نقطة التحول x0 في أقرب وقت ممكن، قبل أن يتسبب عدد المصابين في انهيار النظام الصحي. 

البشر ليسوا جيدين في فهم النمو الأُسّي، فمثلا يمكن أن تؤدي الزيادة البطيئة في عدد الحالات إلى التسبب في شعور زائف بالأمان وتجعلنا نعتقد أننا لسنا بحاجة إلى اتخاذ إجراءات جدية، لكن عندما يصاب عدد كبير من الناس ، يكون الوقت قد فات! لذا كلما أسرعنا في اتخاذ الإجراء المناسب ، كلما حصلنا على نتائج إيجابية أسرع، و هذا ما توضحه الإحصائيات بمقارنة بسيطة بين المغرب وفرنسا مثلا:

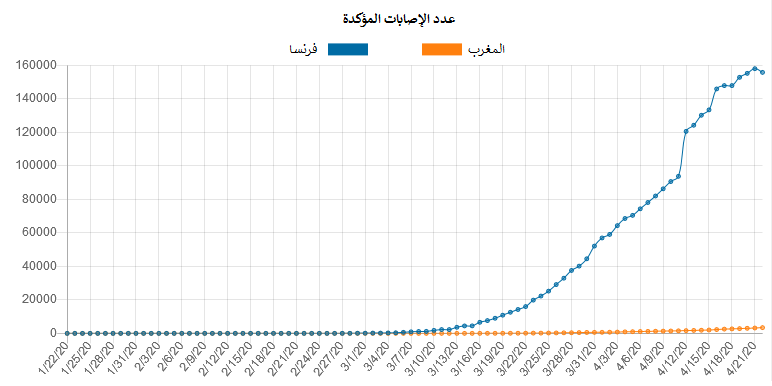
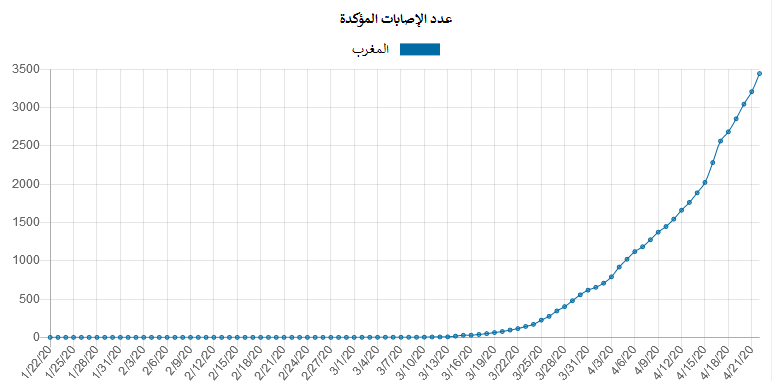
الرياضيات مفيدة بشكل خاص في حالة هذا الوباء. فهي تمكننا من ناحية، من أن نتوقع السيناريو المستقبلي، ومن ناحية أخرى، من اتخاذ الإجراءات اللازمة لتفادي الخسائر والخروج بأقل الأضرار. 

وأول نموذج رياضي و أبسطها هو نموذج (SIR) ، حيث يمكن تقسيم جميع السكان إلى ثلاث حالات: صحية ، مصابة، معافاة. تعتمد دينامية المرض على التبادل بين هذه الفئات الثلاثة، كما توجد أيضًا أمراض لا تحتوي سوى على فئتين: الأشخاص الأصحاء أو المصابين كفيروس نقص المناعة البشرية (VIH).

لكن هل يمثل نموذج (SIR) تطور (Covid-19)؟

الجواب بكل بساطة لا.

تفاصيل هذا الفيروس تتطلب نماذج أكثر تعقيدًا. على سبيل المثال ، من الضروري إضافة متغيرات أخرى كمدة حضانة الفيروس و وجود أشخاص مصابين بدون أعراض والذين يساهمون في انتشار الفيروس.

لذا وجب استخدام نموذج مكون من 4 أصناف والمسمى (SEIR) ، عن طريق إضافة فئة إضافية، الحرف E يمثل الأشخاص المصابين الذين لا تظهر عليهم أعراض حتى الآن.

كيف تتم التبادلات بين هذه الفئات؟

هنا تكمن الصعوبة! يجب اعتبار هذه التبادلات تدفقات زمنية تنتقل من صنف إلى أخر كبعض الظواهر الفيزيائية. هذا الاختلاف في الوقت يسمح لنا بتمثيلهم بفضل المعادلات التفاضلية :

لكن للحصول على ظاهرة الانتشاء الصحيحة ، يجب مراعاة العديد من المعاملات ودمجها في النموذج. أولا يجب أن نأخذ في الاعتبار الاتصالات بين الأفراد التي تختلف وفقًا للفئات العمرية ، والمظاهر الديمغرافية للسكان، فعلى سبيل المثال ، نحن نعلم أن الاتصال بين الأشخاص ليس عشوائيًا تمامًا، فنحن نميل إلى التواصل بشكل أكبر مع الأشخاص في فئة عمرنا ، وأيضًا مع أفراد أسرنا.

باختصار ، هيكل الساكنة مهم جدا في ظاهرة الانتشار ، وسيكون له تأثير بارز علي معاملات نماذجنا، منها المؤشر (R0) مثلا، والذي له عدة أسماء: مؤشر العدوى، ومعدل التكاثر الأساسي ، وما إلى ذلك ، وهو عدد الأشخاص المصابين المتوسط من قِبَل شخص مصاب. و هو مفهوم رئيسي في علم الأوبئة.

ما هي القيمة الحالية لهذا المعامل أو كيف يتم تغيره؟

من الصعب الإجابة عن هذا السؤال بدقة، فعلى سبيل المثال، قيمة (R0) للسعال الديكي أو الحصبة، وهي أمراض معدية جدًا ، تبلغ حوالي 15، أي أن كل شخص مصاب ينقل العدوى إلى 15 فردًا في المتوسط، أما فيروس الأنفلونزا ، فتبلغ قيمة (R0) حوالي 1.5.

بالنسبة لـ (Covid-19) ، فقد تم تقدير (R0) قبل تدابيرالحجر الصحي بقيمة 3، مما يعني أن كل شخص مصاب سيصيب بدوره في المتوسط ​​ما يصل إلى 3 أشخاص. ومع اتخاذ تدابير للسيطرة على الوباء، لم نعد نتحدث عن (R0)، ولكن ببساطة أكثر نتحدث عن معامل التكاثر (R) لأننا اليوم عاجزون على تحديد قيمته بدقة، ويرجع ذلك أساسًا إلى أننا لا نستطيع تحديد عدد جميع المصابين، لذا نعتمد على عدد المصابين المؤكدين فقط.

إذا أصبحت قيمة (R) تساوي 1 ، فهذا يعني أن عدد المصابين أصبح ثابتا. الهدف من الحجر الصحي والتباعد الاجتماعي والتدابير الأخرى هو أن تنخفض قيمة (R) إلى أقل من 1، ونظريا، إذا كان حبس الأفراد كليًّا ، فلن يكون هناك مزيد من الاتصال بين الأفراد ، وبالتالي قيمة (R) ستنخفض للصفر 0 ومدة أسبوعين ستكون كافية لوضع حد للوباء. ولكن هذه الفرضية مستحيلة التحقق تماما.

المراجع: [1] [2] [3] [4]

الكاتب: هشام الشاوش

التدقيق العلمي: مروة بنحاجي