اكتشاف جديد في عالم الأعداد الأولية

تستمر الإكتشافات والمتعة مع الأعداد الأولية، فبعد أن بين أحد الرياضيين أن الأعداد الأولية لا نهاية لها وأنها لن تتوقف عن الظهور، بين رياضيون اخرون أن الفرق بين عددين أوليين يمكن أن يصل إلى 246 عدد فقط. مرحبا بكم في عالم الأعداد الأولية. 

في ماي 2013، بدأ العالم “Yitang Zhang” من جامعة نيوهامبشير  بالبرهنة، ولأول مرة، على أن الأعداد الأولية لا نهائية رغم نذرة الحصول عليها ورغم تباعدها، فلن تتوقف الأعداد الأولية من الظهور، حتى لو كان الفرق بين عددين أوليين 7 ملايين عدد. لكن العديد من الرياضيين حاولوا إثبات ذلك، فتوصلوا إلى أن الفرق بين عددين أوليين يمكن أن يصل إلى 246 عدد فقط رغم وجود حدسية تقول أن هناك مالا نهاية من الأعداد الأولية التي تبتعد فقط بعددين.

الآن، وبعد 76 سنة، بدأ الرياضيون بتحقيق أول تقدم مهم في مجال الأعداد الأولية بطرح السؤال: كيف تتباعد هذه الأعداد؟، “إنه سؤال في غاية الوضوح، لكن الجواب بقي عالقا لما يقارب 80 سنة ” يصرح الباحث في الأعداد ” Andrew Granville” من جامعة مونتريال.

فقد أثبتت مجموعتان من الرياضيين حدسية الرياضي ” Paul Erdős ” حول مدى تباعد الأعداد الأولية، وقد خلصت المجموعتان لتوحيد مجهوداتهما لنشر بحث واحد. ويعتبر “Erdős” واحدا من أبرز رياضيي القرن 20 بطرحه للعديد من المسائل الرياضية،وقد عرض 10.000 دولارا لمن يبرهن حدسيته حول الأعداد الأولية.

ترتكز حدسية ” Erdős” على بحث الرياضي “Robert Alexander Rankin” الذي أثبت أنه من أجل عدد كبير جدا X لدينا: أكبر تباعد (أصغر من X) بين الأعداد الأولية هو على الأقل:

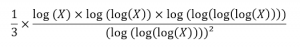
ويصرح “Terence Tao” من جامعة كاليفورنيا بلوس انجلس، الحائز على جائزة الرياضيات “Fields Medal” سنة 2006 (وهي جائزة خاصة بالرياضيات تعادل جائزة نوبل)، والذي شارك في البرهنة على هذه الحدسية أن نظرية الأعداد معقدة لكونها تتوفر على الكثير من دوال اللوغاريتم، ويجد أن مشاركته في البرهنة على هذه الحدسية أمر رائع بحيث أنه إلتقى سنة 1985 بالرياضي “Erdős” في حدث رياضي وعمره 10 سنوات فقط، وتحدث معه حول الرياضيات بجدية كبيرة.

المرجع: [1]