“أويلر” وجسور “كونيغسبرغ”

ليونهارد أويلر بإنجازاته العظيمة في الرياضيات استطاع حل مسائل مستعصية، و وضع فروعا جديدة في الرياضيات. من بين هذه الفروع نظرية المخططات التي ظهرت بفضل عمله في مسألة جسور كونيغسبرغ .

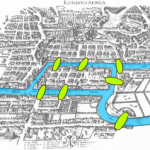
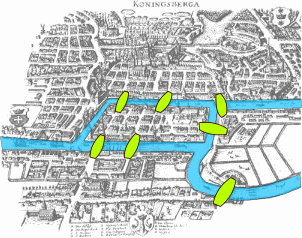
خلال القرن 18 وضع مواطنو مدينة كونيغسبرغ (كالينينغراد حاليا) لأنفسهم لغزا مرتبطا بنهر البريغل الذي يمر وسط المدينة ويقسمها إلى جزيرتين تضمان سبعة جسور كما هو مبين في الصورة. موضوع هذا اللغز كان حول إيجاد طريق عبر المدينة يمر من كل جسر مرة واحدة فقط .

عالم الرياضيات أويلر أدرك أن هذه المسألة تتطلب نوعا جديدا من التفكير . في رسالة كتبها لعالم الرياضيات و الفلكي الإيطالي جيوفاني ماريوني قال أويلر :

” قد يبدو هذا السؤال تافها جدا، لكن من المثير للاهتمام أنه لا الهندسة ولا الجبر ولا حتى الفن فيهم الكفاية لحله. بالنظر في هذا الأمر، تساءلت لو كان ضمن هندسة الموضع التي كان ليبنيز يتوق إليها . وبعد بعض التشاور حصلت على قاعدة رغم بساطتها فإننا عن طريقها نستطيع حل أي مثال كهذا ، بأي عدد جسور في أي ترتيب كان.”

هندسة الموضع عند أويلر نوع من الهندسة لا يهتم بالقياسات الدقيقة للأطوال، والزوايا أو المساحات ، أو ما يسمى حاليا بالطبولوجيا . في مسألة كونيغسبرغ تصميم المدينة في حد ذاته لا يهم . كل ما يهم هو كيف ترتبط النقط ببعضها . باستحضار هذا ، يمكن تحويل الخريطة الفوضوية إلى شبكة منظمة، بنقط تمثل الجزر ، و تمثل الجسور والروابط كما في الصورة.

قام أويلر بملاحظة دقيقة مفادها إذا كان ثمة طريق عبر هذه الشبكة سيمر عبر كل كنقطة مرة واحدة فقط، فإن كل عقدة أو نقطة التقاء يجب أن تملك عددا زوجيا من الروابط ، لأنه عند المرور في العقدة عبر رابط فيجب الخروج منها عبر رابط آخر . إذن ، فهي تحتاج رابطين عند زيارتها مرة واحدة و أربع روابط عند زيارتها مرتين وهكذا دواليك…ومنه فإن العقد الوحيدة التي يمكن أن تملك عدد فرديا من الروابط هي عقد البداية والنهاية.

باعتماد هذه القاعدة، فإننا نعلم أن الطريق الذي نبحث عنه في كونيغسبرغ غير موجودة ، لأن جميع العقد متصلة بعدد فردي من الروابط . يتجلى جمال هذه القاعدة في انطباقها على مسائل أكثر تعقيدا ؛ فمهما كانت الشبكة معقدة أو كبيرة ، فإن طريقا يمر عبر كل رابط مرة واحدة فقط يوجد إذا كانت بعض العقد أو جميعها عدا اثنتين متصلة بعدد فردي من الروابط .

أفكار أويلر حول مسألة كونيغسبرغ كانت بداية ظهور فرع في الرياضيات يسمى بنظرية المخططات أو بنظرية البيان ( graph theory ) .

المصدر: 1

حقوق الصور : Bogdan Giuşcă