علاقة المعادلات العنيدة بالتماثل ونظرية غالوا
قد تتساءلون عن علاقة المعادلات من الدرجة الثانية أو الثالثة المرتبطة بالأعداد بالتماثل المتعلق بالأشكال، وما علاقة كل ذلك بمجموعات الأعداد؟ أو بشكل أدق بنظرية غالوا التي تتحدث عن تمديد الأجسام في الرياضيات “Field extensions“
www.delcampe.com
قد تبدو لكم مصطلحات رياضية غامضة، لذا سنحاول في مقالنا هذا توضيح هذه المفاهيم والعلاقة التي تربط بينها.
سنة 1824 أثبت الرياضي “نيل هنريك أبيل” نتائج مذهلة حول حل المعادلات، وبعدها ببضع سنوات قام الرياضي اللامع “إيفاريست غالوا” بالبرهنة على صحة هذه النتائج كما طور خلال دراسته لهذه المعادلات علاقتها بالتماثل، لكن العالمين معا لم يعيشا طويلا لإعطاء تفاصيل أكثر حول بحوثهما.
حل المعادلات
إحدى أشهر الصيغ الرياضية التي تحدد حلول المعادلة من الدرجة الثانية 
هي: 
و 
مهما تكن الأعداد a و b و c.
كما أن هناك حلولا للمعادلة من الدرجة الثالثة 
إ ما عن طريق التعميل:
وذلك بحل المعادلتين 
و 
أو باستعمال الحل العام للمعادلة: 
والمتمثل في: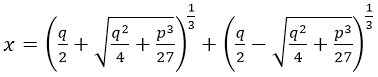 
، أما المعادلات من الدرجة الرابعة فهي بالتأكيد أكثر تعقيدا: 
.
الصيغة التي تعطي حلولا للمعادلات من الدرجة الرابعة أو معادلة من درجة أقل قد تبدو معقدة قليلا (خصوصا عندما يتعلق الأمر بالجذور العقدية) لكنها تستعمل افقط العمليات الأربعة: الجمع والضرب والطرح والقسمة لتمثيل الجذور (أي حلول المعادلة)، السؤال الهام هنا هو: هل يمكن إيجاد صيغة عامة لحلول معادلة من الدرجة الخامسة باستعمال هذه العمليات الأربع فقط؟ أو إيجاد حلول لأيّة معادلة من درجة أكبر؟
النتيجة التي توصل لها العالم أبيل سنة 1824 وبعده غالوا ببضع سنوات أنه لا يوجد حلول من هذا النوع، أي لا يكفي استعمال العمليات الأربع لتحديد حلول عامة معادلة من الدرجة الخامسة، لكن هذا لا يعني استحالة إيجاد حلول لمعادلات خاصة من الدرجة الخامسة، مثل: 
والتي تقبل حلا وحيدا: 
يعتبر غالوا مؤسس نظرية المجموعات والدراسة الرياضية للتماثل مع عمله على المعادلات، عادة ما نتصور التماثل كشيء ماموس: صور أو نماذج متماثلة، لكن ما علاقة التماثلات بالمعادلات؟ الجواب خفي لكنه جميل.
التماثل الثابت
لنتعرف أولا ما هو التماثل، نقول أن الدائرة متماثلة لأننا نستطيع إدارتها 90° أو تغيير محاورها دون أن يتغير شكلها، إذا التماثل هو عدم القدرة على التغير رغم القسام بعدة عمليات على شكل ما، يمكن أيضا التحدث عن التماثل في المعادلات، فمثلا بالنسبة للمعادلة من الدرجة الثانية 
فتقبل حلين متماثلين هما: 
و 
:
لكن ما نوع هذا التماثل؟
لفهم الأمر، سنحلل المعادلة ، لدينا معاملات هذه المعادلة هي 1 و 0 و -2 وهي أعداد جذرية بعكس الحلول و التي هي أعداد لا جذرية، لذا يمكن جمع كل هذه الأعداد في مجموعة واحدة نرمز لها بالرمز 
بحيث تكتب عناصرها على الشكل 
، وهكذا تضم المجموعة الجديدة معاملات المعادلة والحلول معا، أي جميع الأعداد الجذرية (b=0) وحلول المعادلة و (a=0 و b=1أو b=-1) بالإضافة إلى أنها مجموعة تضم جميع الأعداد الناتجة عن عمليات جمع وضرب عناصر تنتمي لها.
المجموعة تسمى “جسم Field” أي ثابتة بالنسبة لقوانين الحسابيات (العمليات الأربع) كما يعتبر أصغر جسم يضم الأعداد الجذرية وحلول المعادلة .
الآن، يمكننا العودة للفكرة الرئيسية حول تماثل الحلين و ، يمكن تعميم فكرة التماثل على الجسم وبالتالي فمماثل العدد 
سيكون هو 
، ويمكن التعبير عن عملية التماثل باستعمال الدالة f التي تحقق: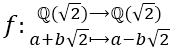 
تطبيق هذه الدالة على جميع الأعداد في لا يؤثر أبدا على بنية الجسم : 
هي فقط تحول الأعداد اللاجذرية إلى مماثلاتها التي توجد أيضا ب، كما أنها لا تمس خصائص الجمع والضرب داخل ، فمثلا: إذا ضربنا العددين و 
سنحصل على:
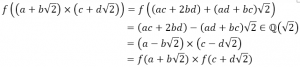
أي عدد ينتمي ل أيضا، وفي هذه الحالة، نقول أن الدالة f هي التماثل المرتبط بالمعادلة
والتي لا تغير على الإطلاق بينة الجسم ، الدالة f تسمى “التشكل التلقائي للجسم 
” ، أي يمكن العودة إلى نقطة البداية بتطبيق الدالة على نفسها (تقابل): 
لكن هل يوجد تشكل تلقائي آخر للجسم ؟ أجل وهو “دالة التماثل Identity fonction g(x)=x “: ، و بنفس الطريقة يمكن تطبيق f على g والعكس:
وهكذا نكون قد شكلنا زمرة تماثل هذه المعادلة (أو مجموعة الأعداد المتماثلة) والتي تعتمد على دالتي التشكل التلقائي f و g ، وهذا هو مبدأ :
“زمرة غالوا للمعادلة Galois Group of the equation”
لكن لماذا لا نستطيع الحصول على حل عام للمعادلات من الدرجة الخامسة؟
يمكننا تطبيق ما سبق على أية حدودية أخرى، مثل المعادلات من الدرجة الخامسة:
بحيث 
أي يمكن تمديد جسم من أعداد جذرية لخلق أصغر جسم 
يضم جميع الأعداد الجذرية وجميع حلول المعادلة (P)، هذا الجسم يسمى “الجسم المشتق للمعادلة Splitting field of P”
يمكننا كذلك ملاحظة التماثل بالجسم المشتق كما فعلنا في المعادلة من الدرجة الثانية، فهناك تشاكل تلقائي للجسم والذي يحافظ على جميع الأعداد الجذرية ثابتة ويدور حول الأعداد اللاجذرية بالجسم ويحافظ على على خصائص العمليات الأربعة، وهذا ما يشكل “جسم غالوا للمعادلة Galois group of the equation P”
ما استطاع غالوا إثباته هو أنه مهما تكن معادلة ما (تقبل حلا باستعمال العمليات الأربع أم لا) فإنها تعتمد على “جسم غالوا”، فإذا استطعنا كسر جسم غالوا إلى عناصر أصغر تضم الجذور المربعة (حلول المعادلة من الدرجة الثانية) أو الجذور المكعبة أو الجذور من الرتبة n فإن المعادلة تقبل حلولا عامة، لكن إذا لم نستطع القيام بهذه العملية أو إيجاد تماثل داخل الجسم، في هذه الحالة لا نستطيع إيجاد حل عام للمعادلة باستعمال العمليات الأربع فقط، وهذا هو الحال مع بعض المعادلات من الدرجة الخامسة وكذا المعادلات من درجة أكبر.
دراسة حل المعادلات باستعمال نظرية المجموعات التي تطرقنا لها هي التي تسمى “نظرية غالوا” الشهيرة.